Simulating bingo for fun
The other day, I was playing bingo with the family. The rules are simple, each person has a 5x5 card with the center number “free”. You pick numbers from 1 to 75 without replacement until some matches 5 in a row on their card (diagonal matches are allowed).
Playing with young kids, I knew there was a clock ticking on how long their attention would last. We had three bingo cards going.
How many numbers would we have to pick for someone to win?
There may actually a closed for solution estimate the mean number of picks for someone to get Bingo with n cards in play. Alas, that is far beyond my remaining math skills. Luckily, I can simply write a Montecarlo simulation. This is about the same difficulty of an Advent of Code problem.
My solution ended up with three classes: board, game, and experiment.
Working on a project like this, I’m still frustrated with code reloading in `irb`. I should probably be able to wire zeitwerk (code loader used in Rails) to accomplish this in the future.
Final solution: playing by yourself you’ll need to pick ~41 numbers on average. And with the three of us, this drops to ~35. So now I have a good idea of how long these games will go on for.
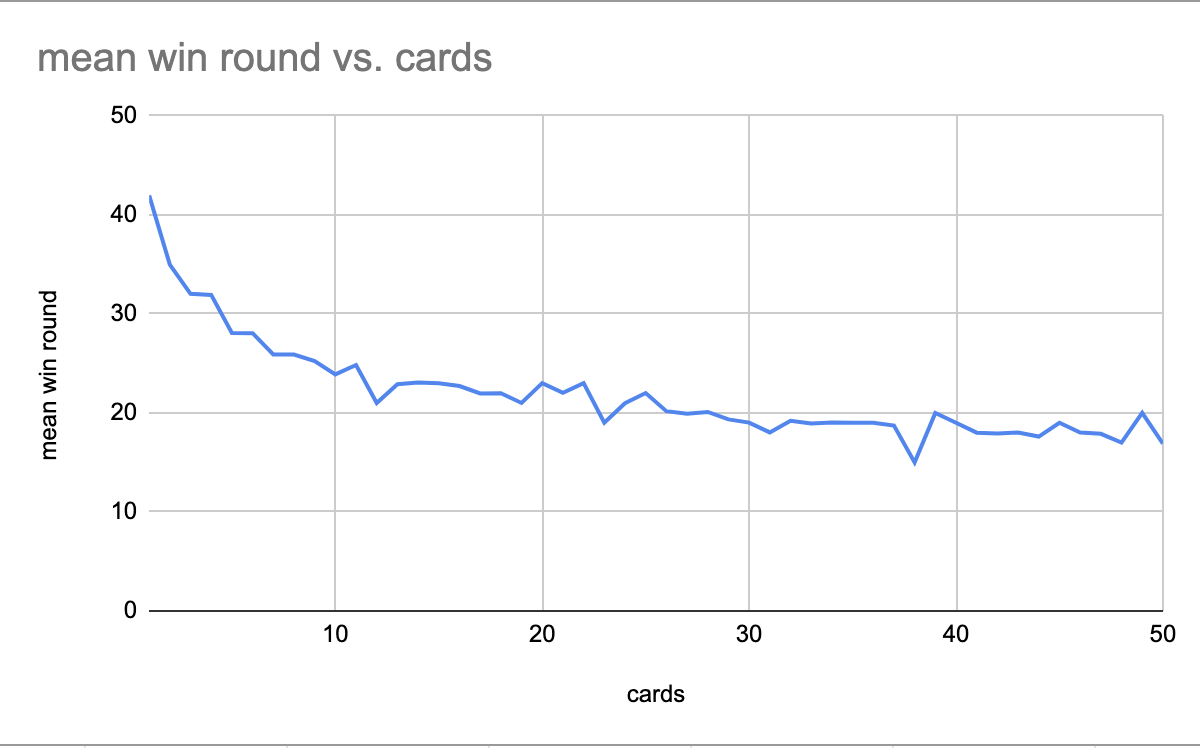
Maybe I'll come back later and add the variance to know how often I’m going to have to wait a lot longer.
Here is the code I wrote to simulate bingo.
Playing with young kids, I knew there was a clock ticking on how long their attention would last. We had three bingo cards going.
How many numbers would we have to pick for someone to win?
There may actually a closed for solution estimate the mean number of picks for someone to get Bingo with n cards in play. Alas, that is far beyond my remaining math skills. Luckily, I can simply write a Montecarlo simulation. This is about the same difficulty of an Advent of Code problem.
My solution ended up with three classes: board, game, and experiment.
Working on a project like this, I’m still frustrated with code reloading in `irb`. I should probably be able to wire zeitwerk (code loader used in Rails) to accomplish this in the future.
Final solution: playing by yourself you’ll need to pick ~41 numbers on average. And with the three of us, this drops to ~35. So now I have a good idea of how long these games will go on for.

Maybe I'll come back later and add the variance to know how often I’m going to have to wait a lot longer.
Here is the code I wrote to simulate bingo.
module Bingo
class Experiment
def run(epsilon = 2, boards=1)
@games = []
last_mean = 0
while true do
@games.push Game.new.play(boards)
mean = @games.sum.fdiv(@games.size)
if (mean-last_mean).abs < epsilon
return mean
end
last_mean = mean
end
end
end
class Game
def initialize
reset
@i = -1
end
def play(board_count=1)
boards = board_count.times.map { Board.new }
5.times { draw }
while(boards.none? { |b| b.win?(drawn) }) do
draw
end
@i
end
def drawn
return [] if @i < 0
@pulls[0..@i]
end
def draw
@i+=1
drawn
end
def reset
@pulls = pulls
end
def pulls
1.upto(75).to_a.shuffle
end
end
class Board
attr_reader :board
def initialize
# order col, row
@board = init_board
end
def win?(picks)
full_picks = picks + [0]
return true if match?(full_picks, diag_1)
return true if match?(full_picks, diag_2)
0.upto(4).each do |i|
return true if match?(full_picks, col_vals(i))
return true if match?(full_picks, row_vals(i))
end
false
end
def match?(a1, a2)
(a1 & a2).length == 5
end
def to_s
@board
end
def pretty
0.upto(4).each do |i|
puts row_vals(i).map { |c| c.to_s.rjust(3) }.join
end
end
def col_vals(j)
@board[j]
end
def row_vals(i)
@board.map { |c| c[i] }
end
def diag_1
@board.map.with_index { |c, i| c[i] }
end
def diag_2
@board.map.with_index { |c, i| c[4-i] }
end
private
def init_board
5.times.map do |i|
if i == 2
(i*15+1).upto(i*15+15).to_a.shuffle[0..3].insert(2, 0) # center is always a match
else
(i*15+1).upto(i*15+15).to_a.shuffle[0..4]
end
end
end
end
end
# write out a CSV to stdout
puts "cards,mean win round"
1.upto(50) do |i|
result = Bingo::Experiment.new.run(0.001, i)
puts "#{i},#{result}"
end